地球は、表面の約70%が海で覆われている惑星。 太陽系でただひとつ、生命が確認されており、 自身の1/4の大きさである衛星"月"を引き連れています。 スポンサーリンク 目次地球の大きさ(直径・面積・質量)ってどのくらい?71 万有引力 97 図72 月の落下と円運動 が成り立つ.これから重力が距離r にどのように依存するかを考察しよう. 円運動の角速度を!中学生は加速度を学習しないので,正しい重力の求め方を教えられないのですが,みなさんはすでに加速度について学習しています! 「100gあたり1N」という中学校で習ったことは忘れて (これ重要!) , W = mg で正しい重力の大きさを求められるようにし

面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス
地球の面積速度 求め方
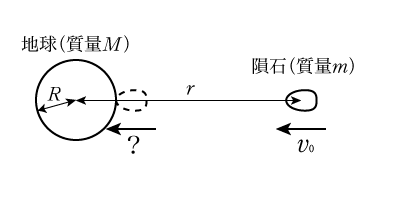
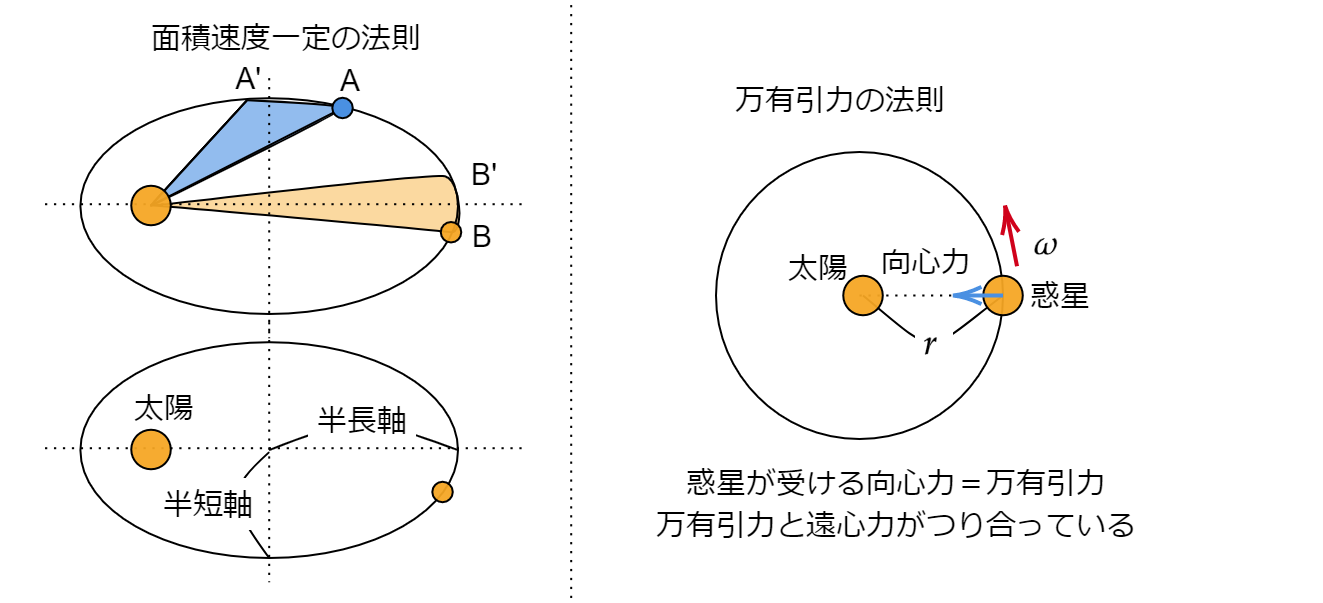
地球の面積速度 求め方-T だけ変化 するので,惑星はr × !万有引力による式 F=G Mm/R² がつりあっている。 g重力加速度98m/s² R地球の半径≒64×10⁶mが分かっていることを前提に M=g×R²/G (M地球の質量)が求められます。 *半径の求め方はここでは割愛 しかし、公式も生み出されていなかった時代



ケプラーの法則とは 問題での使い方まで徹底解説 受験メモ
地球が太陽から単位時間あたり受け取るエネルギー量 は、半径 * の球面を通過する太陽の全放射エネルギーのうち、地球の断面積分のみが地 球に吸収されるとして求められる。すなわち、 ! 面積速度が惑星の軌道上の速度を求めることであれば 軌道上の速度をV、太陽天体の距離r 、惑星の平均距離a、として r,aを天文単位、Vの単位を天文単位/年、M=1とすればG=4π^2ですから 軌道上の速度Vを求めるには V=√ (4π^2 ((2/r) (1/a))) です。 かくして、R、g、Gが求められ、地球の密度ρを求めることができ、結果的に、 M = 4ρπR 3 /3 の式で地球の質量が求められたわけです。 ちなみに、上で使った数値を代入して計算すると、有効数字2桁で、 ρ = 55×10 3 (kg/m 3) M = 60×10 24 (kg) となります。
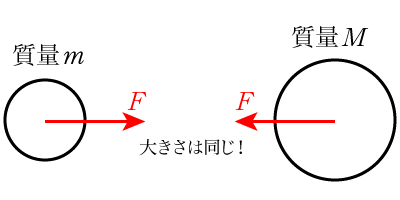
万有引力の法則 ニュートンが発見 ニュートン* かの有名なアイザック・ニュートンのことです。 1642年~1727年、イギリス。物理学の祖といえる人です。 閉じる は、惑星が太陽のまわりを回り続けるのは、惑星と太陽との間に引力がはたらくため* 引力が無ければ2つの物体は離れ離れになっ身近で遠い月の量り方 付かず離れず地球の周囲を回り、夜空にひときわ明るく輝く月。 その質量は、はかりに載せたわけでもないのに、約7千京トン(京は10の16乗)であることがわかっています。 いったいどうやって量ったのでしょうか。 17世紀、天体地球の総面積は × 10 6 km 2 で、そのうち海が3622 × 10 6 km 2 (地球表面の711%)、陸地が × 10 6 km 2 (同2%)である 。 陸地は地球表面全体に均等にではなく 北半球 に偏って分布しており、陸地の多い側を 陸半球 (りくはんきゅう)、海の多い側
日射量s↓:地球上における熱輸送量の大きさは太陽定数を基準に するとわかりやすい。太陽定数とは,太陽と地球が平均距離のとき, 地球大気の上端において,太陽光線に垂直な単位面積に単位時間に 入射する太陽エネルギーi 0 のことで,102 角運動量保存、ケプラーの第2法則 図102 面積速度 (103)の第2番目の式は簡単に積分できる: 1 r d dr (r2θ˙)=0これより r2θ˙ = const = S (104) が導かれる。図102から分かることは、S は太陽 と惑星を結ぶ線分が単位時間に掃く面積の2倍で11 答え 111 時速 (km/h) を求めるので、まず365日を時間 (h) に直します。 12 時速10万キロで




ケプラーの法則まとめ 理系ラボ




高校物理 ケプラーの第二法則 映像授業のtry It トライイット
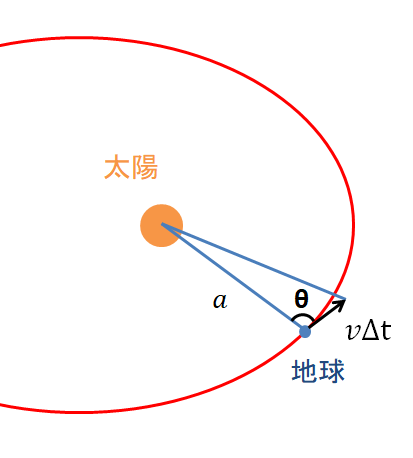
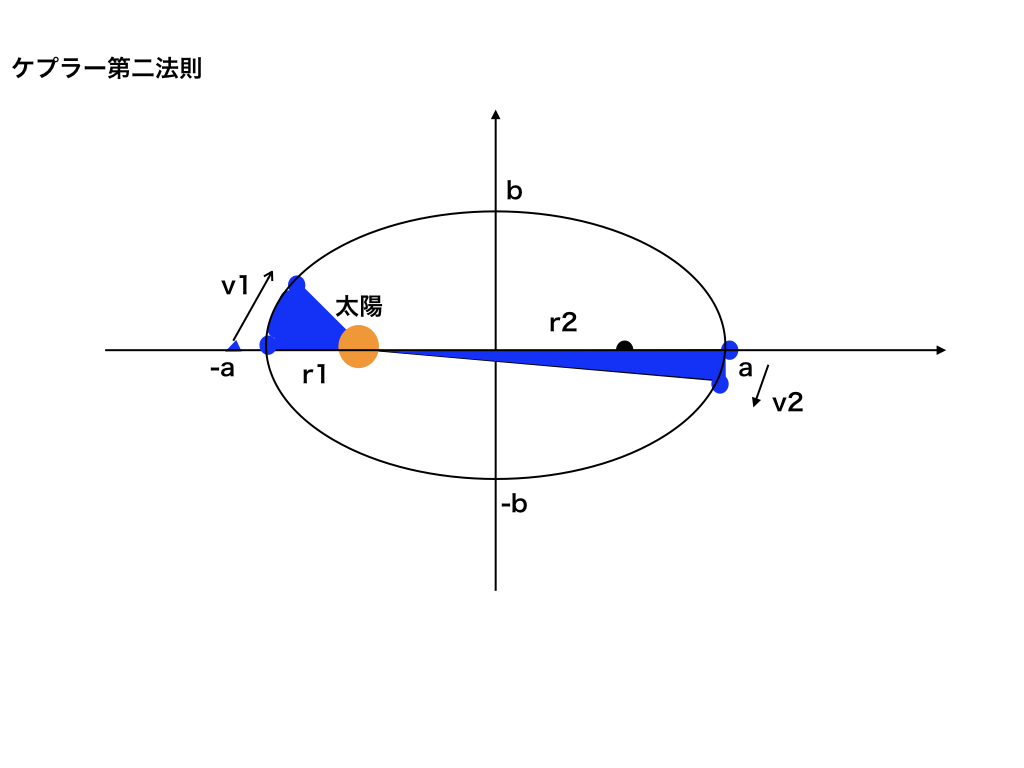
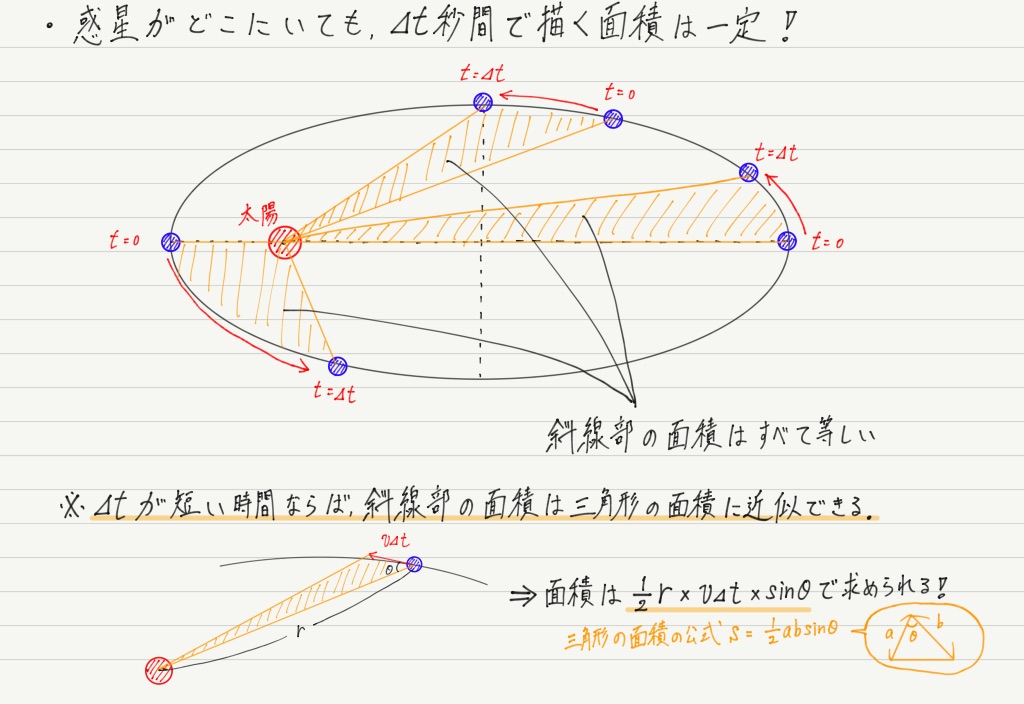
地球上の全海洋面積をSs=Km 2 とすると、陸上の氷がすべてとけ、海洋に流出した時の海面上昇高さ(H)は(7)式となる。 H = Vw/Ss ・・・ (7) 図2の様に、エクセルを用い海面上昇高さを計算すると、約375mとなった。 この面積速度は次の式で示すことができます。 動径長さ r 、惑星の速さ ⅴ 、動径と速度がなす角度の大きさを θ 、としましょう。 そうすると図の三角形の面積が面積速度を表しています。一般に, 面積 速度 は ベクトル であって, 原点 O に関する動点の 位置ベクトル を r ,速度を v とするとき,面積速度は次式で与えられる。 ここで, m は動点の質量, l は r × mv で,原点に関する角運



二体問題 Two Body Problem
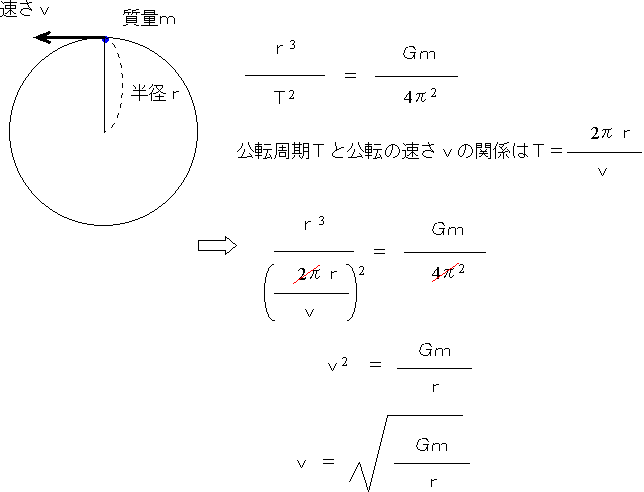



太陽系その他の天体
地球の大きさと形 18世紀前半にフランスは、低緯度地域(ペルー)と高緯度地域 (北欧)に測量隊を派遣し、天文緯度1°あたりの距離を測定 その結果、高緯度の方が1kmあまり長いことが判明 →地球の形は、扁平な回転楕円体積速度一定)から, F ϕ = 0 (715) であることがわかる。すなわち,ケプラーの第2法則から,惑星が太陽から受ける力はr 方 向成分F r だけを持つことが導かれる。 ここで,面積速度一定から,保存する量を h = r2 dϕ dt (716) と置く。 定義 面積速度とは,下図に示す が単位時間あたりに掃引する面積である. 導出 微小時間 間に,点 の座標が, から へ移動したとする. このとき, が掃引する面積を とすると, は次のように表わされる. (が十分小さいとき,)



2 25 極座標の微分方程式




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス
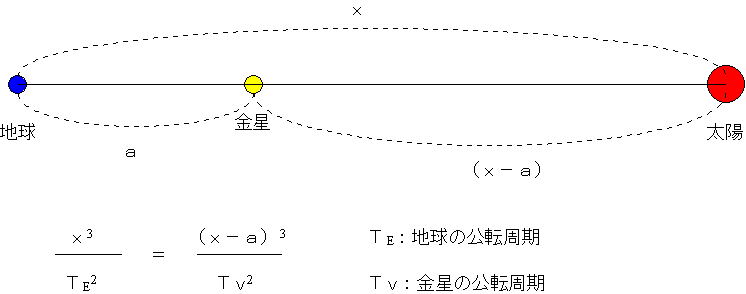
地球の公転周期 e= 365日 火星の公転周期 p= 687日 を用いる.地球と火星の角速度の差に会合周 期sを掛けると,火星に対して地球の進んだ 角が360°となるから,公転周期は以下のよ うに計算できる. 360 360 1 1 1 360 779 2 16 2 2 s e p e p s sEx 7–1 月の半径は地球の1/4 であり,質量は1/100 である.月面上での重力加速度を求めよ. Ex 7–2 それぞれの質量がma およびmb の二つの天体a およびb が互いに引き合って円運動をしている. 回転の中心から天体a およびb までの距離をそれぞれra およびrb とするとき次の問に答えよ.環境によっては表示速度が遅くなる場合がありますが、ご了承下さい。 1 地球をながめてみると そもそも経緯度は、地球上の任意位置を指し示す手段として考え出されました。下の図のように、地球の南北の中心に赤道があることはご存じですね。



物理 古典力学の基礎 惑星の運動 技術情報館 Sekigin 最も身近な惑星の運動に関連し 楕円軌道 ケプラーの法則 万有引力に項目を分けて紹介する




ケプラーの第一 第二 第三法則をどこよりもわかりやすく解説
面積の定理 面積速度:動径OP が 単位時間に掃過する面積 面積POP' をdt で割ると 面積の定理: 1つの質点が 固定点から中心力の作用を受けて運動するとき, 力の中心のまわりの面積速度は一定である 40 (一定) j j = = 11 2 22 1 2 r d r dt h Q r dr y x O P r j P' dj66 第6 章 中心力のもとでの運動 面積速度 時刻t に位置r にあった質点が,微小 時間後のtΔt にrΔr に移動したとする。 微小 時間Δt のあいだに位置ベクトルが掃いた面積ΔS は,r とΔr を2辺とする三角形の面積で近似でき る(図63)。 Δr の大きさをΔr と表し,r とΔr とのなす角を磁界と荷電粒子の速度が垂直で ない場合、ローレンツ力は磁束密度 と速度の作る平行四辺形の面積に 比例した力となる。よって、 負の電荷に働く力 磁界と速度が垂直でない場合 磁束密度B 速度v F qvBsin ab ab cos ab ab sin 力F vsin



ケプラーの法則とは 問題での使い方まで徹底解説 受験メモ



万有引力とケプラーの法則 物理の学校
面積速度 面積速度とは何だ? 面積速度 図に示すとおり、微小時間dtの間に質点がPからp′のように働いたとする。PからOP′に下した垂線をPHとすれば、dθは微小角なのでPH=r dθとなる。従って、dtの微小時間に動径が掃過する面積は、 となる。り,葉や植物体の正味の光合成量を土地面積あたりで表 す場合には,これを純一次生産(Net primary production:NPP)と呼ぶ.1960年代から7 0年代の初めにかけ て,陸上生態系だけでなく,海洋・湖沼などの地球上の 面積速度一定の法則はニュートンのプリンキピアの中にもその記述・解説が見られ、ニュートンの思想に多大な影響を与えています。 この面積速度一定の法則から、角運動量保存則が導かれるのです。 ここで言う角運動量とは、質量×動径×速さ で示され



地球や水星の面積速度の求め方は また計算に使用する固有時は Yahoo 知恵袋



高校物理 元 理学部物理学科が教える ケプラーの法則 宇宙 Spacenuts
太陽・地球間の距離: 1.5 x 10 11 m ゆえに、地球の公転速度は約 3.0 x 10 4 m/sとなります。光の速度が 3.0 x 10 8 m/sとなりますから、地球は太陽の周りを光の速度の1万分の1の速度で公 転していることが判ります。T だけ移動する.一方,速さで書くと移動距離は 角度× 半径=弧の長さ実習「地球軌道の離心率を求めよう」 クセル単位で光球の視直径を求め、グラフ化する。 (3)視直径の比較 約1 年分の、10日毎の光球視直径の変化を調べ、最大値と最小値を 7.実習の進め方 (1) 白色光太陽全面像(fits 形式)のダウンロード 国立天文台




高校物理 シンプルにまとめよう 万有引力 力学 お茶処やまと屋



Www Tsuyama Ct Ac Jp Imgver4 Kyousyokuin Kiyou Kiyou18r03 Pdf
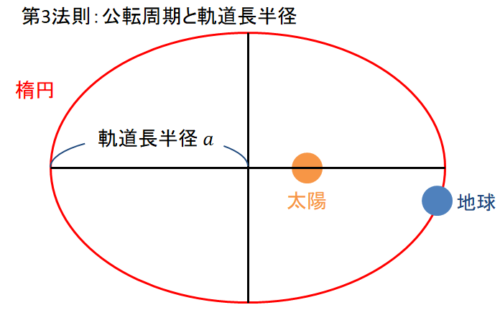
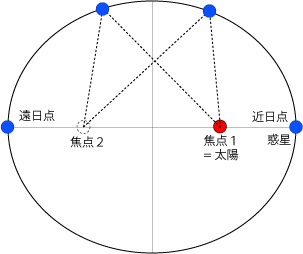
逆に、13年や16年は下弦の前後ですから、月は太陽に近い方へ地球は太陽から遠い方へ移動していくため、地球の近日点通過は地球-月重心の近日点通過よりも早くなります。 関連ページ † こよみ用語解説;求められる。楕円の面積は であり、面積速度は で一定であるから軌道周期 は となり、 と を入れれば 或いは となり、惑星の周期の二乗が軌道長半径の三乗に比例するというケプラーの第三法則が導かれ固定する.小球 A に初速度を 与えたところ,A は O を中心とし て半径 l の円周上を角速度 ω で等速円運動した.このとき,A の角運動量はいくらか.糸の張 力 T はいくらか. (2) この状態で B を静かに l/2 だけ 引き下げて固定した.この時 A




13 ケプラーの第三の法則 長半径 3 K 公転周期 2 里山コスモスブログ



ケプラーの法則ってなに わかりやすく解説 受験物理ラボ




ケプラーの法則まとめ 理系ラボ
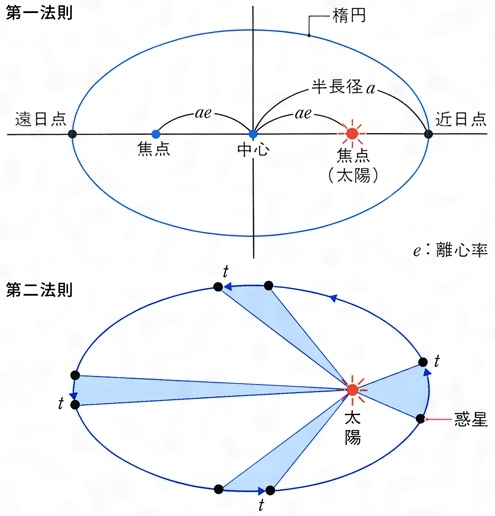



ケプラーの法則とは コトバンク




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス



ケプラーの法則 わかりやすい高校物理の部屋



ケプラーの第二法則 面積速度一定の法則 の求め方
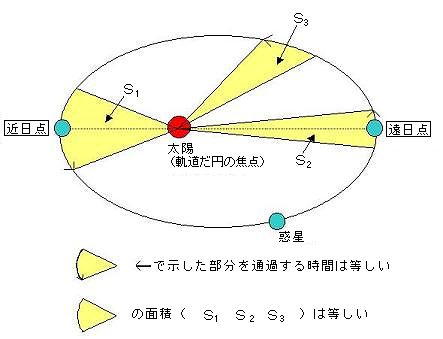



実験地学 10



面積速度一定の法則 高校数学 高校化学 高校物理に関連した基礎の基礎の復習です
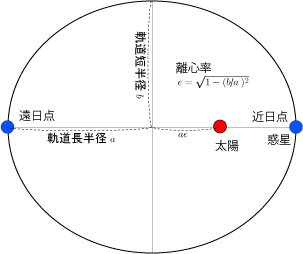



暦wiki ケプラーの法則 国立天文台暦計算室



Adoko 力学 ケプラーの法則




高校物理 ケプラーの法則 Youtube




万有引力むずい 教えてください Clear




ケプラーの法則 Wikipedia




2 学年 物理 人工衛星 5 1 第一宇宙速度 5 2 人工衛星



ケプラーの法則とは 問題での使い方まで徹底解説 受験メモ




ケプラーの法則とハレー彗星 Koko物理 高校物理




ケプラーの法則 高校物理の備忘録




高校物理 シンプルにまとめよう 万有引力 力学 お茶処やまと屋



ケプラーの3法則 物理のかぎしっぽ



面積速度一定の法則っていうのは 惑星の楕円軌道でなく 地球上の Yahoo 知恵袋
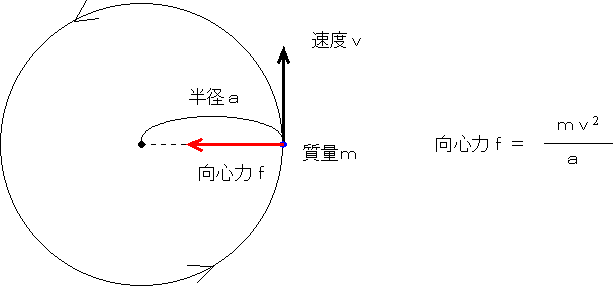



太陽系その他の天体



1




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス



ケプラーの第二法則 面積速度一定の法則 の求め方




高校物理 ケプラーの第二法則 練習編 映像授業のtry It トライイット



Q Tbn And9gctnocnbispupw9wcbhh8rcgeqb3fc Kw21fmrehorpde36zoh Usqp Cau
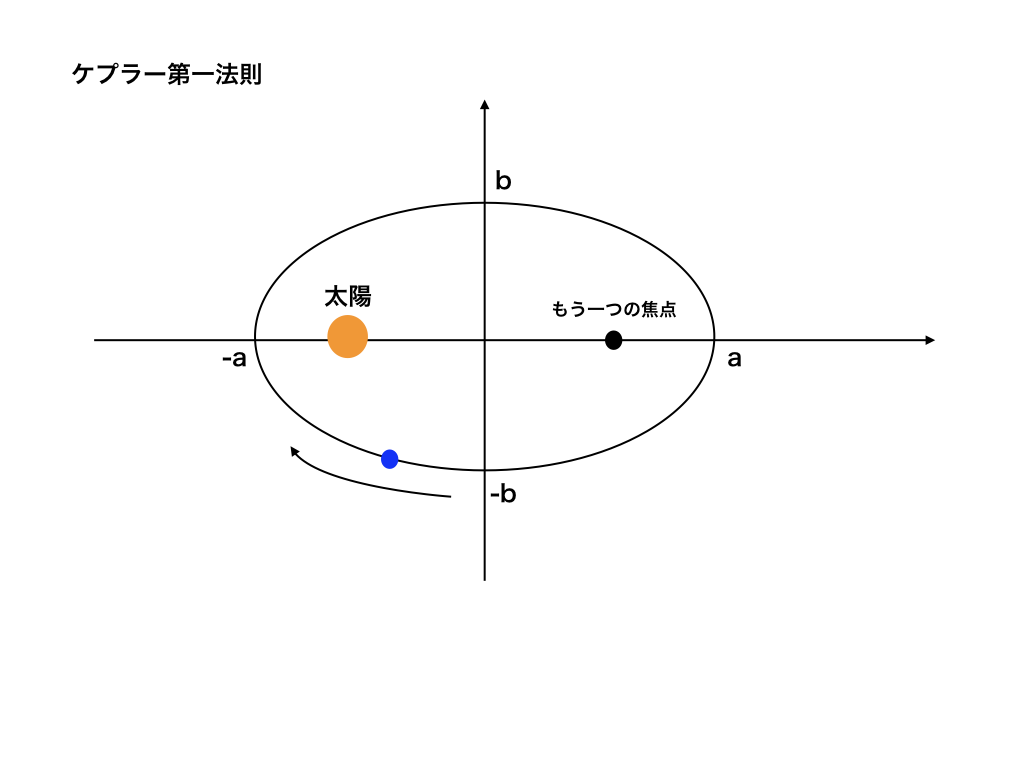



ケプラーの第一 第二 第三法則をどこよりもわかりやすく解説



Kakeru Movie
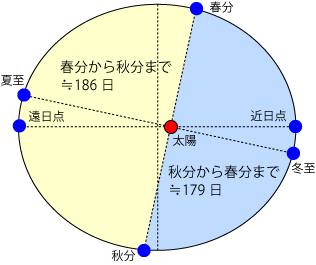



暦wiki ケプラーの法則 国立天文台暦計算室



地球や水星の面積速度の求め方は また計算に使用する固有時は Yahoo 知恵袋




ケプラーの法則と万有引力 3つの法則をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ



中大理工物理 08年 2




ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に




万有引力むずい 教えてください Clear
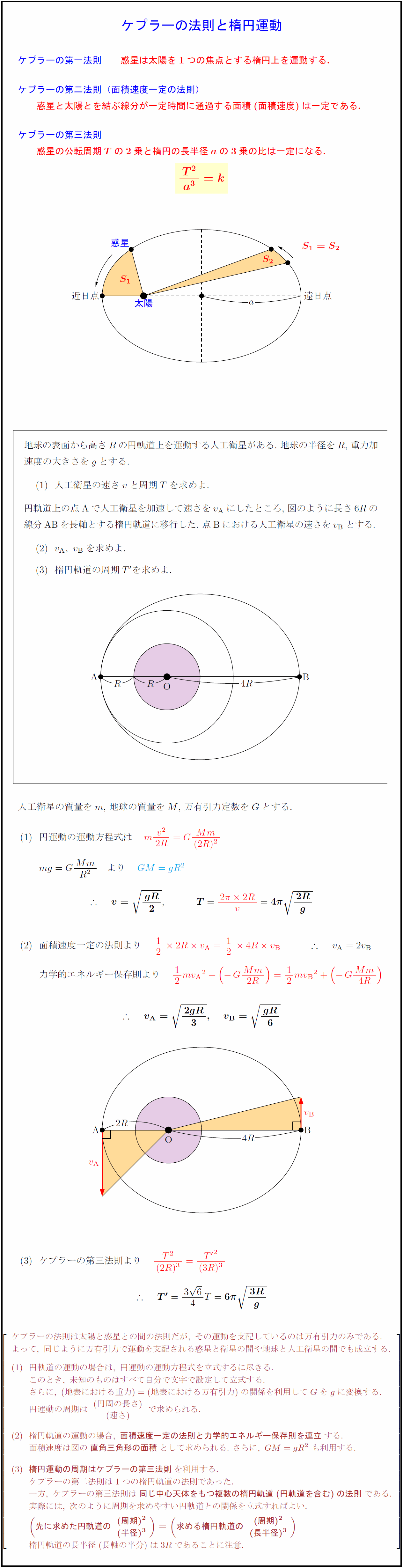



高校物理 ケプラーの法則と楕円運動 受験の月




高校物理 ケプラーの第三法則 映像授業のtry It トライイット




簡単解説 ケプラーの第1 第2 第3法則とは 3分でわかる 宇宙ラボ




ケプラーの法則とハレー彗星 Koko物理 高校物理
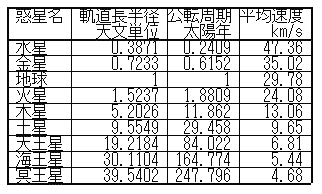



学生読み物 人工天体の運動学




地球はどのくらいの速さでまわって 自転して いるの 自然 科学なぜなぜ110番 科学 学研キッズネット




ケプラーの法則とは ぷち教養主義




ケプラーの 面積速度一定の法則 を理系ライターが解説 天体の観測から到達した物理法則 Study Z ドラゴン桜と学ぶwebマガジン




ケプラーの 面積速度一定の法則 を理系ライターが解説 天体の観測から到達した物理法則 Study Z ドラゴン桜と学ぶwebマガジン
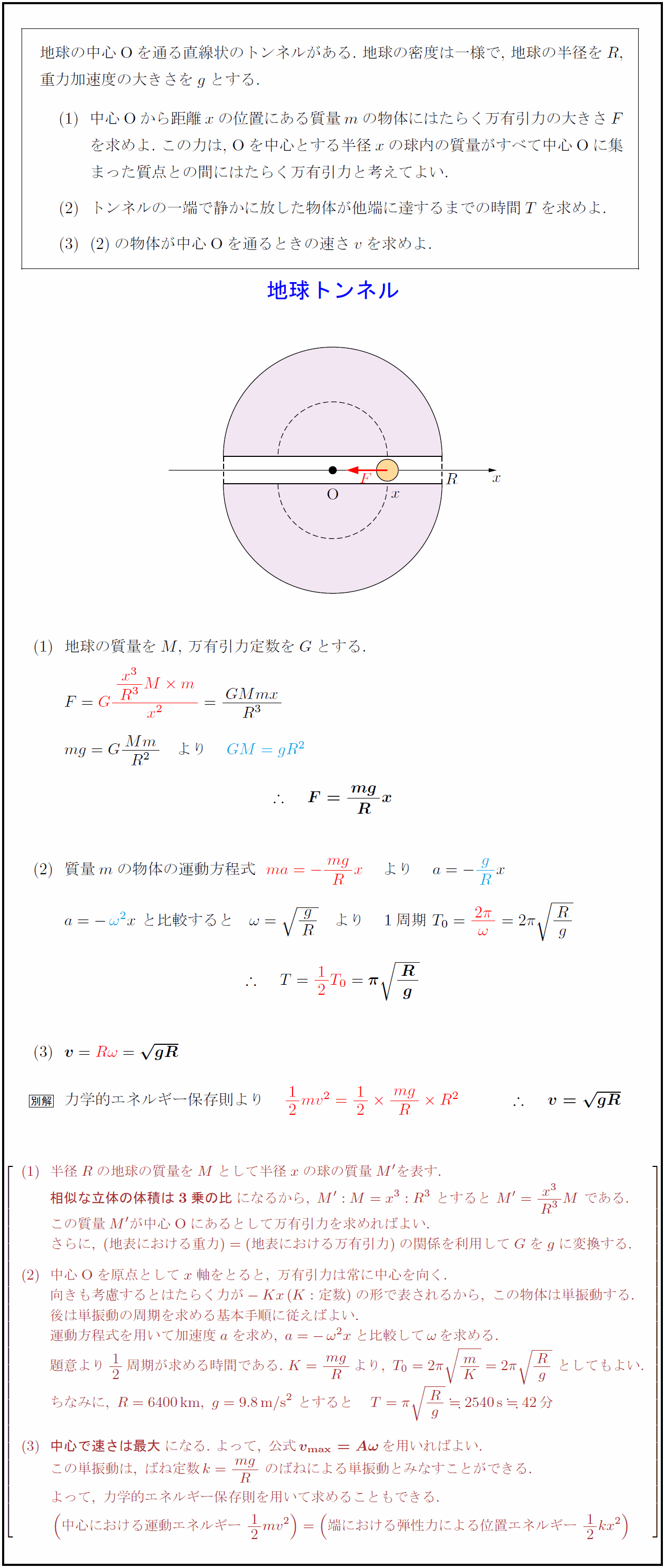



高校物理 地球トンネル 万有引力による単振動 受験の月




面積速度一定の法則 惑星の運動について ケプラーの第二法則の解説がわから Okwave




太陽系その他の天体
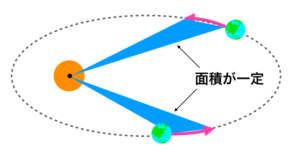



ケプラーの法則ってなに わかりやすく解説 受験物理ラボ



Q Tbn And9gctwwondhom4qzc3am0bbnqtx0vev1e 5dcqx6r0xfso8pxh6jg7 Usqp Cau
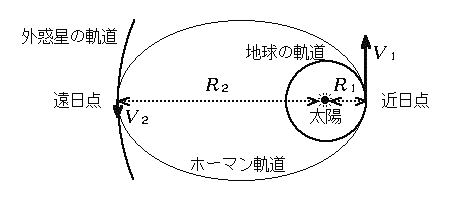



学生読み物 人工天体の運動学




ケプラーの法則 高校物理の備忘録



ケプラーの法則




力学 ケプラーの第二法則 面積速度一定の法則 Youtube



ケプラーの法則 雲外蒼天



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora
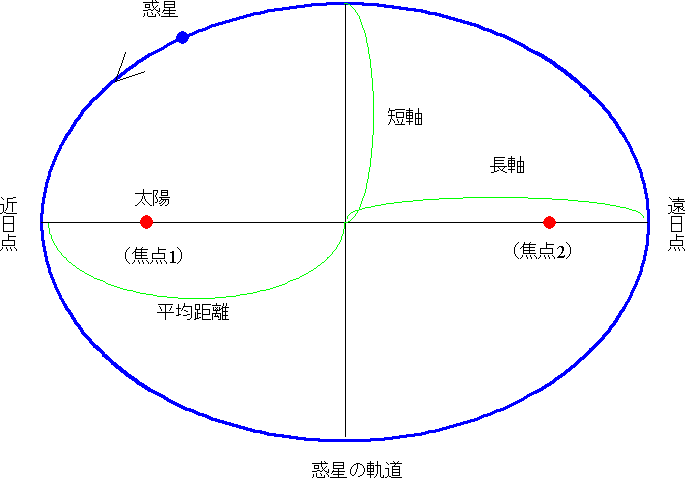



太陽系その他の天体




面積速度一定の法則 入試に出る3つのパターン 証明 年の東大でも出題 Physicmath フィジクマス




ケプラーの法則と万有引力 3つの法則をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ



ケプラーの法則 わかりやすい高校物理の部屋



惑星の軌道計算をするには面積速度一定の法則を使うと思うのですが どのように解けばよいのですか Quora



万有引力とケプラーの法則 物理の学校



高校物理 元 理学部物理学科が教える ケプラーの法則 宇宙 Spacenuts



ケプラーの第一 第二 第三法則をどこよりもわかりやすく解説



3




ケプラーの 面積速度一定の法則 を理系ライターが解説 天体の観測から到達した物理法則 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン




ケプラーの法則まとめ 理系ラボ



暦wiki ケプラーの法則 国立天文台暦計算室
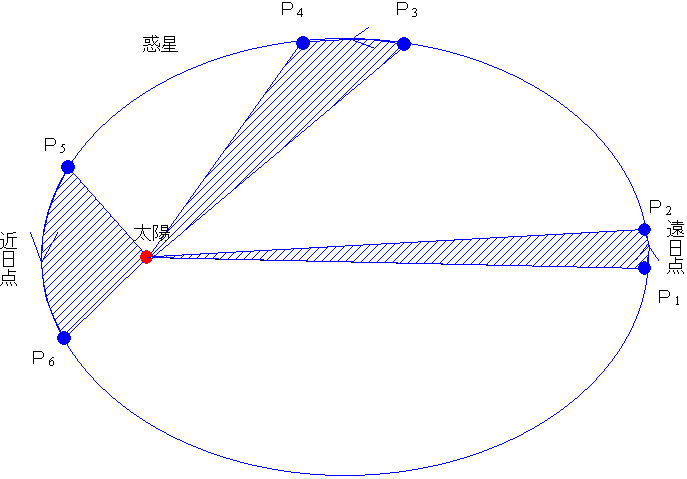



太陽系その他の天体



ケプラーの法則とは 問題での使い方まで徹底解説 受験メモ




グランドエスケープ 19年の年末に 太陽の死角に立ちこの地球 ほし を出るのに必要な速度 第三宇宙速度 を求めてみる Qiita




中心力問題 惑星の運動や角運動量保存則 Ocean



楕円軌道とケプラー方程式 Kepler Equation
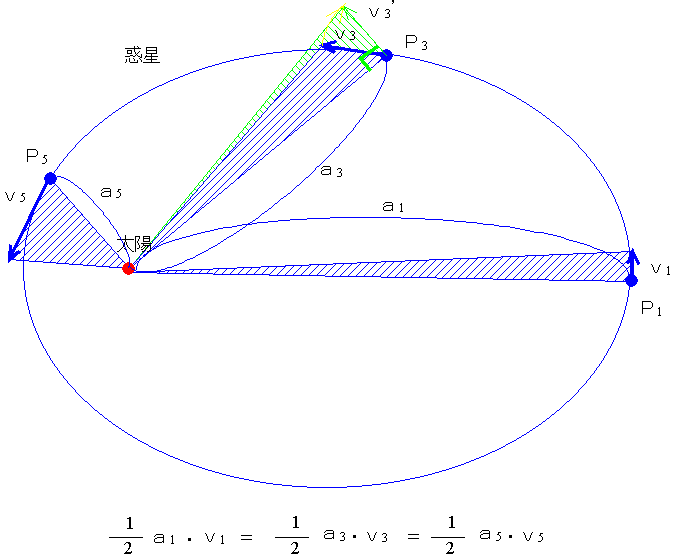



太陽系その他の天体




高校物理 ケプラーの第二法則 練習編 映像授業のtry It トライイット



理科年表で計算 計算結果 太陽の寿命 E mc2 彗星のスピード 地球のスピード 彗星の周期 水星の付近の明るさ 金星の付近の明るさ 火星の付近の明るさ 軌道計算 楕円覚書き 静止軌道半径 光の速さの測定 レーマー 遠近点距離と速度の関係 物理
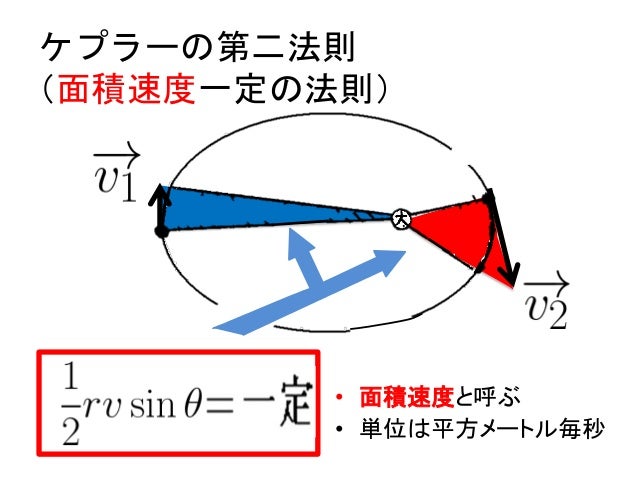



惑星の運動




太陽 木星 月の質量を求める計算 惑星物理基礎ノート Planetscope
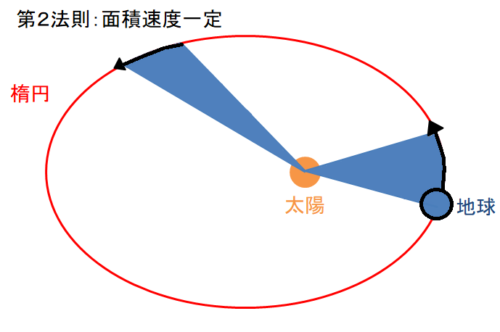



高校物理 元 理学部物理学科が教える ケプラーの法則 宇宙 Spacenuts



ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に




太陽 木星 月の質量を求める計算 惑星物理基礎ノート Planetscope



ケプラーの第2法則 面積速度一定の法則 サラリーマン 宇宙を語る



太陽系その他の天体




ケプラーの法則 高校物理の備忘録




ケプラーの法則 Wikipedia



1 10万有引力 受験の物理屋さん




ケプラーの法則と万有引力 3つの法則をわかりやすく解説 高校生向け受験応援メディア 受験のミカタ



プトレマイオス天動説のエカントとコペルニクス地動説の周転円



あなたと自然科学 関連の講義情報 第1部



ケプラーの法則 高校物理をあきらめる前に 高校物理をあきらめる前に



0 件のコメント:
コメントを投稿