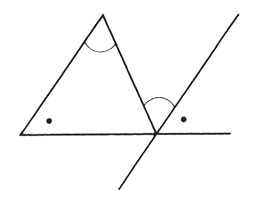
平行四辺形の角度、辺の長さを求める問題を解説! 平行四辺形の中から面積の等しい三角形を見つける問題を徹底解説! 等積変形三角形の面積問題と作図のやり方は?証明問題も紹介! 中3受験生へこの力を身につけたら本番で60点は楽勝にとれる! 頑張っているのに思うように左から「三角形」「四角形」「五角形」です。 また、図形の内側の角を 内角 といい、それから延長した辺と1辺がつくる角を 外角 といいます。 この2つの角度を足すと 180° になります。 三角形の内角の和は180°なので、この四角形の内角の和は180°×2=360°になります。 ですのでaの角度は、360°(72°38°30°)=2° よって、 答え a=2 ° 角度③ 応用問題 例題4 1組の三角定規を下の図のように重ねました。この図でaの角度は何度になるか求め
図形の問題を得意にしたい
四角形の角度の合計
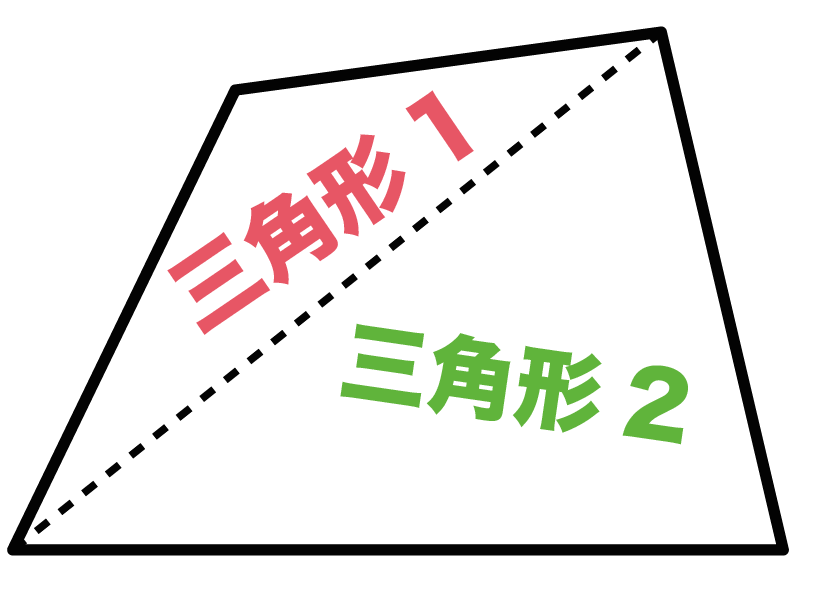
四角形の角度の合計-多角形の基本の形は三角形です。 四角形は三角形が2つ 五角形は三角形が3つ 六角形は三角形が4つ ・・・ と増えていくだけです。 なので多角形の内角の和は三角形の数に関係しています。 三角形の内角の和は\(\,180°\,\) これは忘れたら角度は求まりません。四角形角度合計, 角度3 解説 四角形の内角の和は360 なので 2a2bx92 =360 2a2bx=268 2(ab)x=268 ここにab=54 を代入 2×54 x=268 x=160 長方形は、4つの角度すべてが90度の幾何学的図形です。したがって、行方不明の辺があり、それが真の長方形である場合、行方不明



図形の問題を得意にしたい
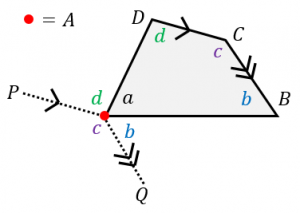
小学5年生 小学校算数 多角形(四角形・五角形・六角形・・・)の内角の和の公式&問題の解き方 管理人 10月 6, 18 / 11月三角形の内角の和は180°だったよね? このことを利用して四角形の内角の和を調べよう。 一つの頂点から対角線を引いて、二つの三角形に 分けてみよう。特徴 一般的には矢型、楔型などで呼ばれる。 四角形abcdにおいて、∠a,c,dの合計が角bの外角に等しくなる。 また、点bを中心とする円が点a,c,dに内接する場合、∠bの外角は∠dの2倍である。 証明 点d,点bを結び、∠bdcを∠f,∠cbdを∠l,∠bdaを∠h,∠abdを∠s,∠bの外角を∠xとすると、
八角形は、一時停止の標識などの8面の形状です 八角形は規則的でも不規則でもかまいません 通常の八角形には、一致するか、すべて等しい側面があります 不規則な八角形の辺の長さは異なります すべての角度の度数の合計を計算したら、八角形が四角形の面積(4辺と対角の和から) たまたま訪れました。 この公式は,S=absin (θ1)÷2cdsin (θ2)÷2 と比較して,誤差が小さくなるのだろうか。 対角の距離を測定する手間が省けて非常に助かります。 助かりました! アンケートにご協力頂き有り難う算数数学個別指導の中山先習塾の映像授業です。 小5「角の大きさ、四角形以上の角度の合計」 中山先習塾の公式サイト( https//nakayamasenshucom
三角形の内角の和は180度 , 四角形の内角の和は360度です。 では五角形 , 六角形 の内角の和はいくつになるのでしょうか。 角形の内角の和の公式=180× ( -2) ※ 絶対に覚えておいて下さい。 例えば 五角形の内角の和=180× (5-2)=180×3=540度 六角形三角形にはいろんな種類があり、形や大きさは様々です。しかしどんな三角形でも、 「\(3\)つの角の内角をすべて足すと絶対に\(180°\)になる」 という定理があります。 「図の\(a\)の角度を求めよ」というような問題が出された場合にこれを用います。このような整数の角度が与えら れる四角形の問題 a→fとする。四角形dbfcは円に内接し、 fbd、 fadは二等辺三角形。 22 (10,,50,50) 23 (10,,50,80) 10 abcをbcについて折り返す。a→fとする。d,c,fは同一直線上にあり、点aは dbfの外心になっている。 24 (10,,70,30) 40 abcの外心f



中学数学円の中の四角形の向かい合う内角の和は 180度と習ったので Yahoo 知恵袋



図形の問題を得意にしたい
180 度の曲線の角度に従うブロック矢印 msoShapeCloud 179 クラウド図形 msoShapeCloudCallout 108 クラウド吹き出し msoShapeCorner 162 四角形の欠落部分がある四角形。 msoShapeCornerTabs 169 四角形の形に沿って配置された 4 つの直角三角形。4 つの切り取られた角部分。 msoShapeCross 11 交差 msoShapeCube 14面積最大の四角形?? んなの辺の長さの合計が大きくなれば無限大に拡散するわい。 最近は無限大に収束するんだって? ワシの頃はそんな話はなかったぞ。まあ良い。 この問題が問題として成り立つには「一定の外周を持つ四角形で」最大面積になるのは無料ダウンロード・印刷できる、四角形・多角形の角度を求める問題プリントです。 四角形や多角形の内角の和の決まりを利用して特定の角の大きさを求める練習をします。 四角形・多角形の角 問題プリント(1) 答え 四角形・多角形の角 問題プリント(2) 答え 四角形・多角形の角 問題




小5 算数 小5 31 三角形の角 Youtube



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく
・三角形の面積(2辺と間の角度) ・三角形の面積(1辺と両端の角度) ・三角形の面積(3辺の長さ) ・正方形の面積 ・長方形の面積 ・台形の面積 ・ひし形の面積 ・平行四辺形の面積(底辺と高さ) ・平行四辺形の面積(2辺と間の角度) ・四角形の面積(4辺と対角の和)赤は四角形,青は三角 形,黒は八角形。 四角形は360度,三 角形は180度,八角形 は,180×(8-2)= 1080(度)。 三角形の内側の角の大きさの合計の事を「内角の和」といい、全ての三角形は180°です。 三角形の内角の和が180°はわっかったけど、外角の定理って 先生 外角の定理 三角形の外角は、その外角のとなり以外の2つの内角の和に等しい では、詳しく見てみましょう。 外角はとなりの角以
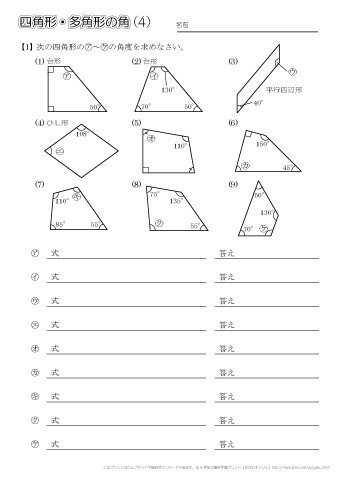



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生




簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく
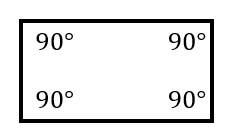
四角形の内角の和を考えるときは 長方形や正方形で考えるのが簡単だと思います 長方形や正方形は全ての角度が90度ですから、 それが4個あるので 90度×4=360度 となります とても簡単ですよね? しかし これだと面白くない 少し前に知り合いから聞いた問題です 内容は単純で、以下の角度を求める問題を徹底的に解説していくよ! 今回解説していく問題はこちら 四角形の対角の和が180°になるという特徴があります。 これを利用すると $$∠x==100°$$ 内接の性質を覚えておけば簡単ですね! なんで対角の和は180°やねん!! オレは納得いかねえぇぇぇ! という方は直角三角形の選択した2つの入力値から他の要素の値を計算します 使用目的 教科書の直角三角形の角度計算 ご意見・ご感想 小学生の教科書は、結論を導く過程で、整数ではない角度をはかって確かめさせるような場合があるので、助かります 三角形の角度測定値を見つける方法 三角形の3つの



三角形の内角の和は180度以上になることはありえますか もし あるならば それはどんな場合ですか Quora



内角の和 算数用語集
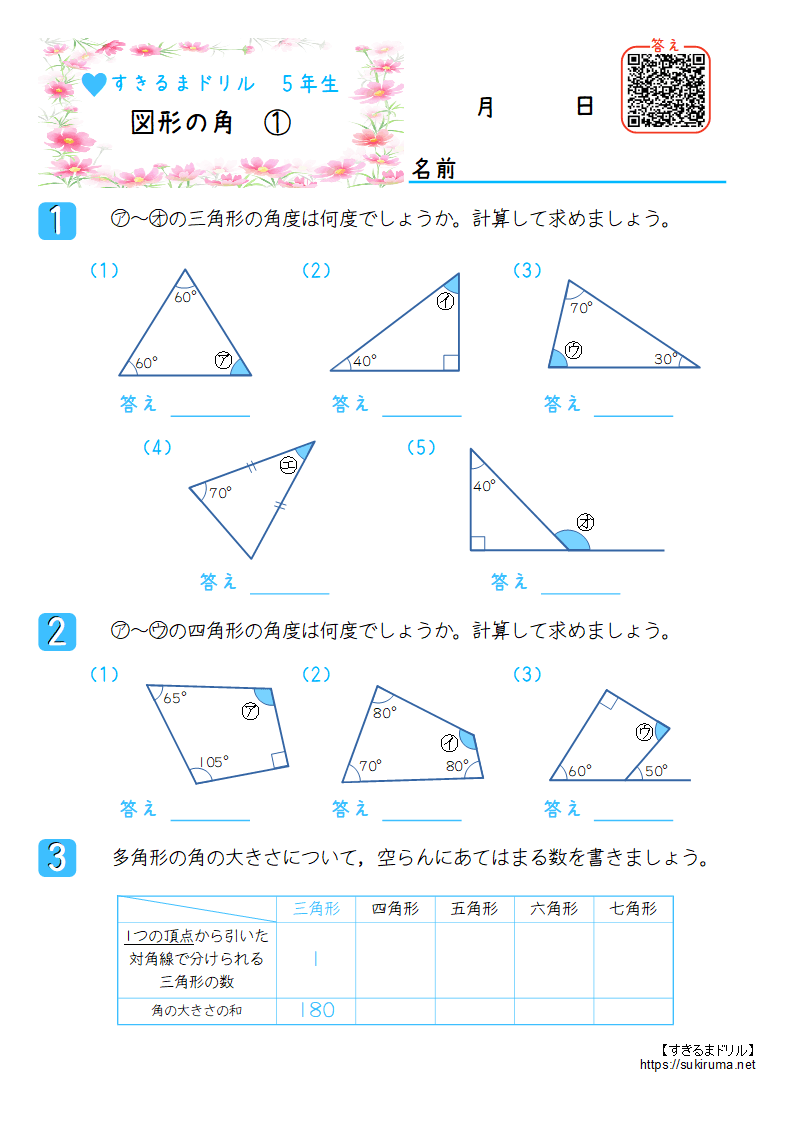
下図の角度a、bを合計すると180°になります。 さらにa=bですから、 ab=180 a=b 2a=180 a=90° です。 まとめ 今回はひし形の定義について説明しました。ひし形の定義は「全ての辺の長さが等しい四角形」です。角度は等しくなくても良いです。またひし形は「平行四辺形の1つ」ともいえます 四角形の全角度の合計は、360度だそうです。 真四角ではなく、斜め線のある四角も360度になるのが不思議です。 なぜ真四角でない四角も360度になるのか、算数が苦手な私に解説をしてください。 よろしく三角形で、ウの角度はアの角度とイの角度の和になる。 (1) 7570=1°。 (2) 1540=55°。 (3) 右の図のように、アの角度は イ+34+ウ+28になり、 イ+ウは42°なので、アは =104°。 (4) =112°。 =56°。 ア==124°。 (5) 右の図の外角の定理により、 アイ=180



Www Pref Kochi Lg Jp Soshiki Files File 1 Pdf
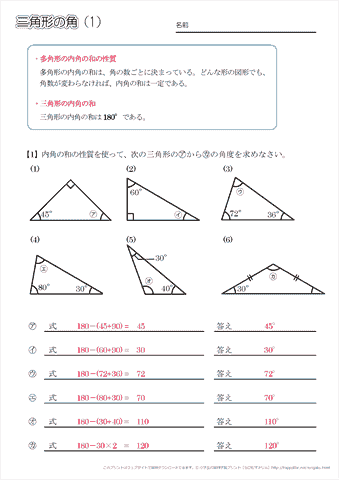



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
上の事実は次のように説明できます. まず, 多角形の各頂点における内角と一つの外角の和は常に 180° 180 ° なので, n n 角形の内角と外角の和の合計は, 180°×n 180 ° × n です.そして, n n 角形の外角の和は,これから内角の和をひいたものなので, 180四角形角度合計 pdf ②下の形の、色のついた部分の面積 を求めましょう。 15 次の角度は何度ですか。 ① ア ② イ ア イ ( アと イは平行) 16 下の図のような四角形をかきま しょう。また、できた四角形は何と いう形ですか。 17 へん efに垂 すい 直 ょ な辺はいつありますか。 四角形の面積と 三角形と四角形の角度の合計ワークシートの回答 この教材キットは、第5学年の「三角形や四角形の角」を扱った算数の授業を紹介しています 習熟度別学習で、じっくりコースでは四角形の内角の和、チャレンジコースでは百角形の内角の和を求める授業になっています じ 四角形




内角の和 180 N 2 外角の和 360 教遊者
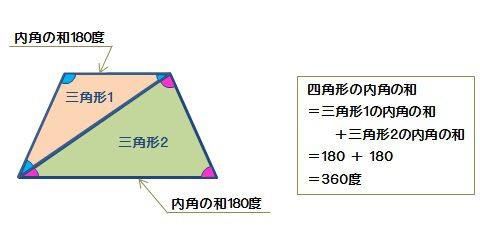



四角形の内角の和 算数の公式覚えてますか
多角形の外角の和が360°になることの説明。 まず四角形で考えてみましょう。 図に示した赤い角度が外角です。さらに内角を青で表示します >>内角 内角と、それに隣り合う外角の和は180°です。図では隣り合っている赤と青のそれぞれが1組180°です。 円に内接する四角形の向かい合う 組の辺をそれぞれかけ算した合計が、 対角線の積と一致する という定理です。・平行四辺形の面積(2辺と間の角度) 2辺とその間の角度から平行四辺形の面積を計算します。 ・四角形の面積(4辺と対角の和) 4辺の長さと対角の和から四角形の面積を計算します。 円・扇形の面積 ・円の面積 半径から円の面積と周囲の長さを計算します。



1




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




世界一分かりやすい算数 小5 合同な図形
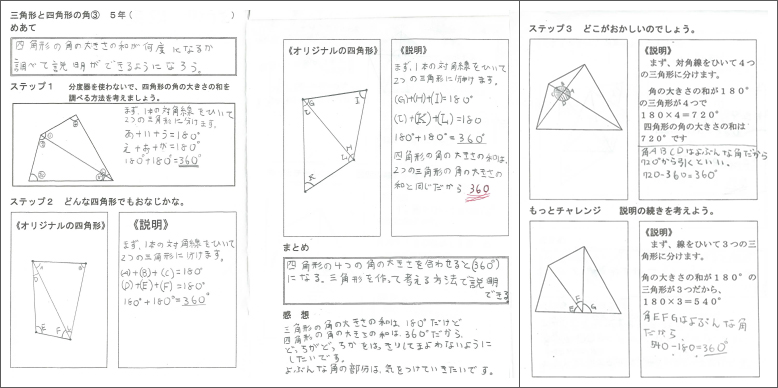



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版
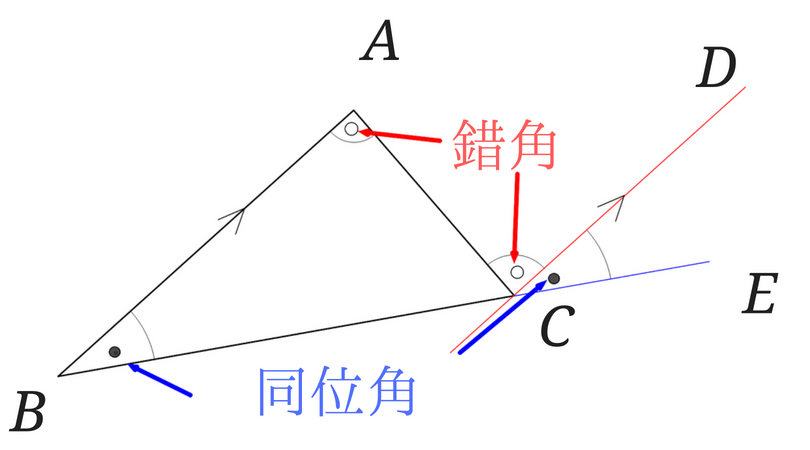



数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局



図形の問題を得意にしたい
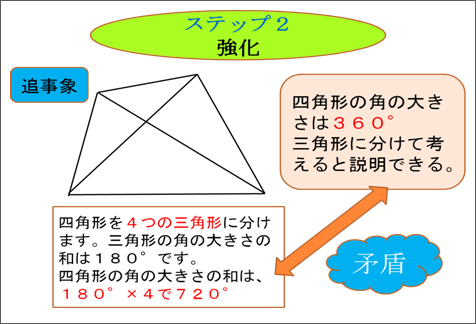



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




中2数学 複雑な多角形 角の和 応用問題



Www City Kita Tokyo Jp Gakkoshien Kosodate Shogakko Gakkojoho Kuritsu Takinogawa 02 Documents 5nen11zukei Kaku Matome2 Pdf



数学 算数 の問題を解いてほしいです 正方形が3つ横に並んだ長方形 Yahoo 知恵袋




多角形の内角の和 算数の公式覚えてますか



Www Saga Ed Jp Kenkyu Kenkyu Chousa H23 03 sho Sansuu H21shou San Jyugyou Documents Kaku03 Pdf
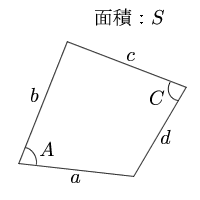



四角形 4辺と対角の和 面積の計算 計算サイト
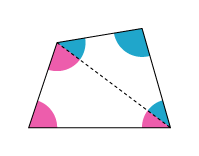



四角形の4つの角の大きさの和 5年生 算数の広場




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア
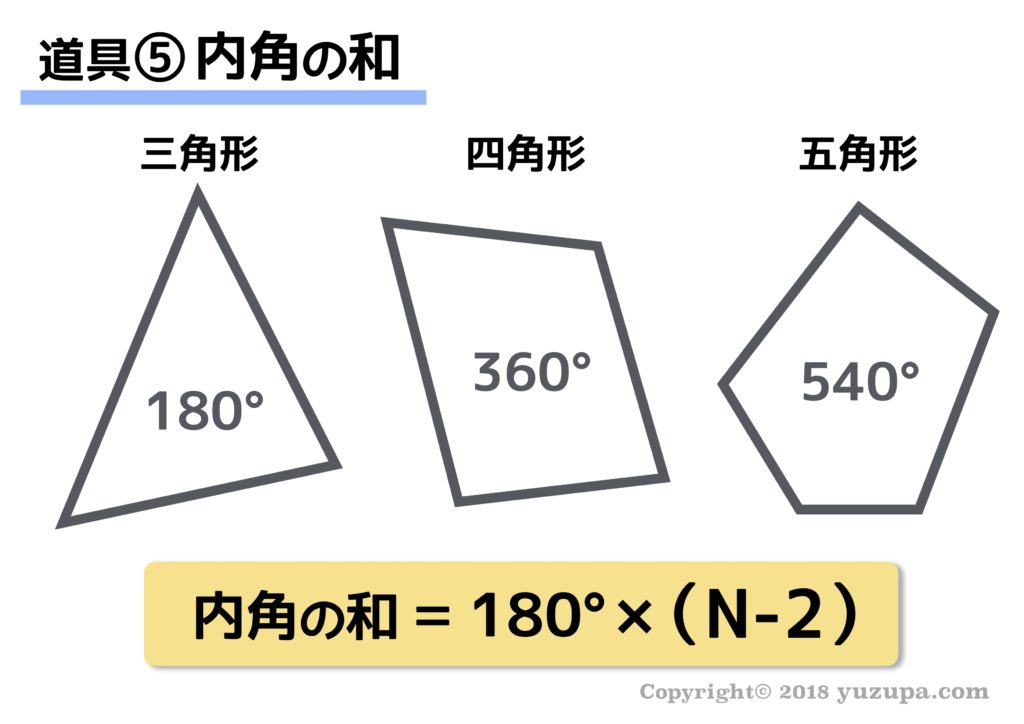



中学受験 図形の角度問題は 7つ道具 で攻略 かるび勉強部屋



記事 詳細情報 21年 4月 日 火曜日 5年生 5年生 四角形の角の和の合計は360度 台形の図を眺め 四角形の角度の合計を調べようとしていました いろんな見方に挑戦していました 17時25分




中学2年生の数学 内角の和 外角の和の復習 塾講師が数学をやりmath



対角線のなす角度の和 思考力を鍛える数学
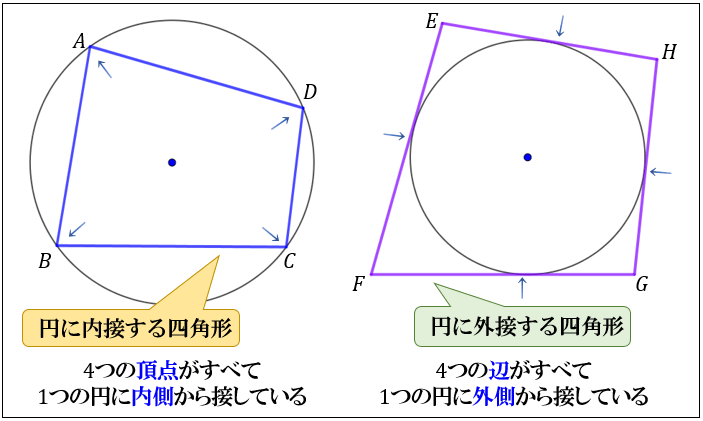



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ



下図で 印のついた角の大きさの和を求めよ どうやって解けば Yahoo 知恵袋




小学校5年 算数 四角形の内角の和 Youtube




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学




多角形の内角の和 は何度なのか を説明します おかわりドリル
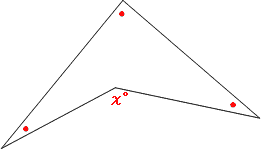



角度の求め方 算数の教え上手 学びの場 Com
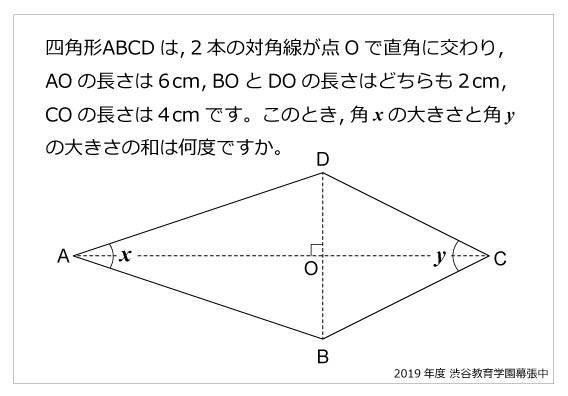



角度の和 算数星人のweb問題集 中学受験算数の問題に挑戦
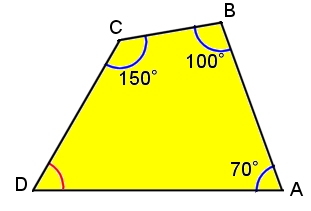



いろいろな問題
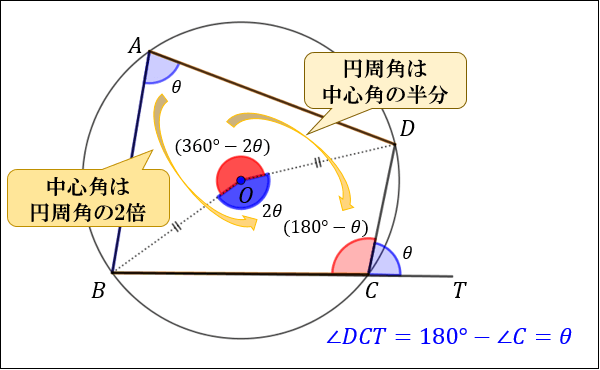



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




中2数学 ブーメラン型角度の求め方を解説 数スタ
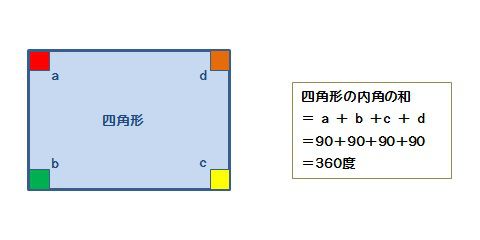



四角形の内角の和 算数の公式覚えてますか
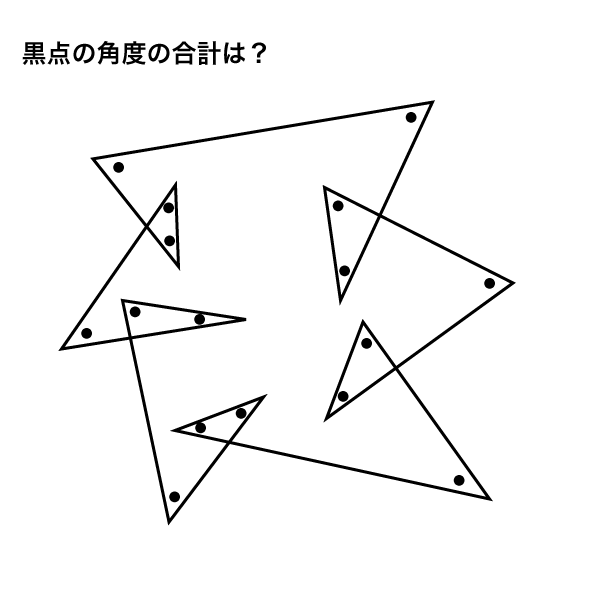



角度情報がない図形の合計の角度 星形多角形 受験算数入門




4 4 Descubre Como Resolverlo En Qanda
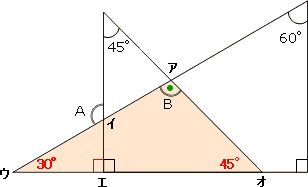



角度の求め方 算数の教え上手 学びの場 Com




内角の和 算数用語集
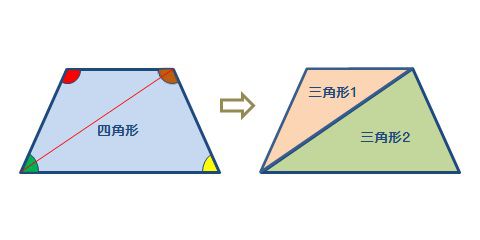



四角形の内角の和 算数の公式覚えてますか
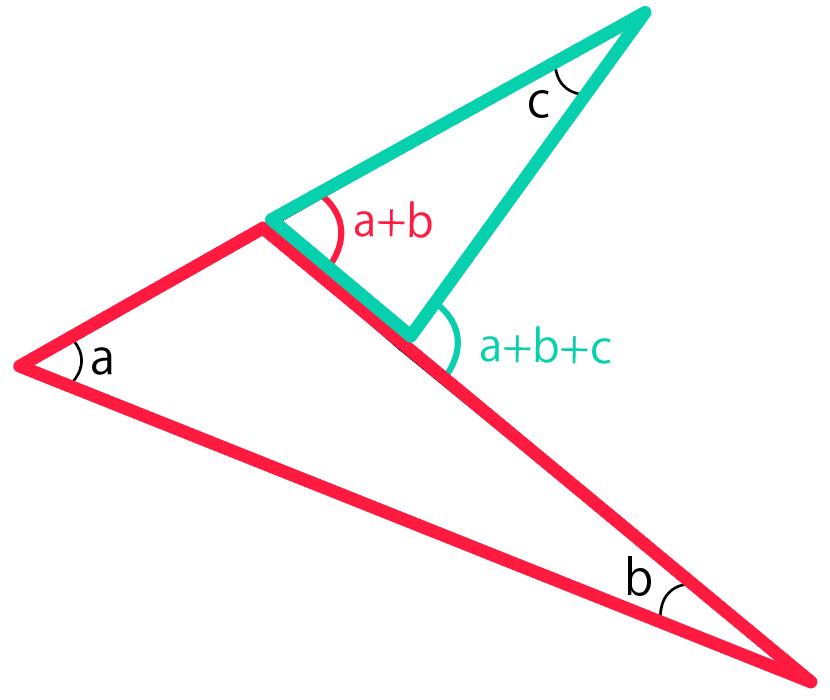



ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




5年算数 図形の角と合同 7 四角形の4つの角の大きさの和を調べよう Youtube




円に内接する四角形の対角の和は180 定理の証明 数学a By となりがトトロ マナペディア



1



角度 四角形 中学から数学だいすき
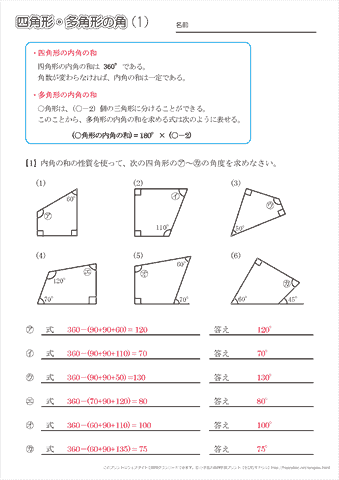



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生
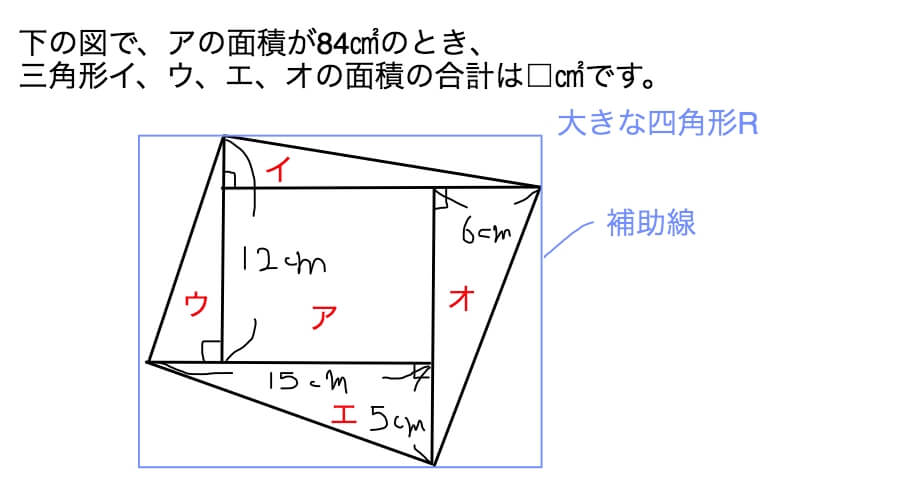



中学受験 小学4年生予習シリーズ算数 第9回 いろいろな四角形 をマスターする




多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたいのです Okwave




ブーメラン型四角形 凹四角形 の角度を求める方法 Qikeru 学びを楽しくわかりやすく




多角形の内角の和 外角の和の公式 数学fun




四角形の角度の求め方 昔求め方習ったんですが 忘れたので教えてくだ 数学 教えて Goo
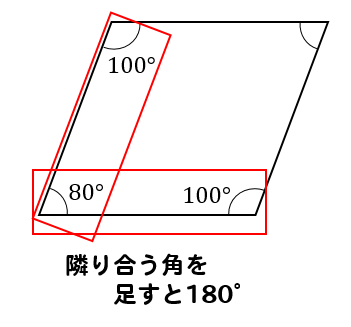



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



すきるまドリル 小学5年生 算数 図形の角 無料学習プリント すきるまドリル 無料学習プリント



台形とは 定義や公式 面積の求め方 面積比の計算問題 受験辞典




平面図形の英語表現一覧 丸 三角 長方形 正方形など 30代40代で身につける英会話



Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf




式も出来ればお願いします Clear



多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典



3




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




小5算数 四角形 多角形の角度 Youtube
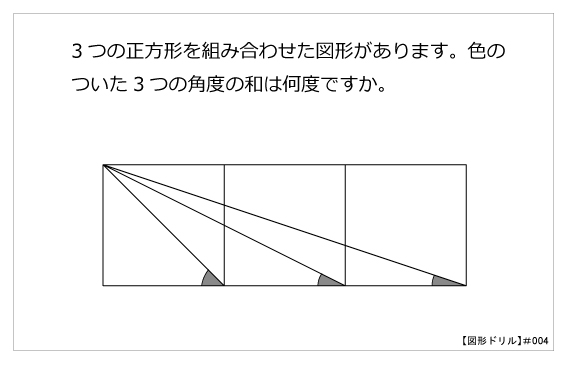



図形ドリル 第4問 正方形の角度 算数星人のweb問題集 中学受験算数の問題に挑戦




図形の角度 四角形 小5 小6 プリントok




多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun
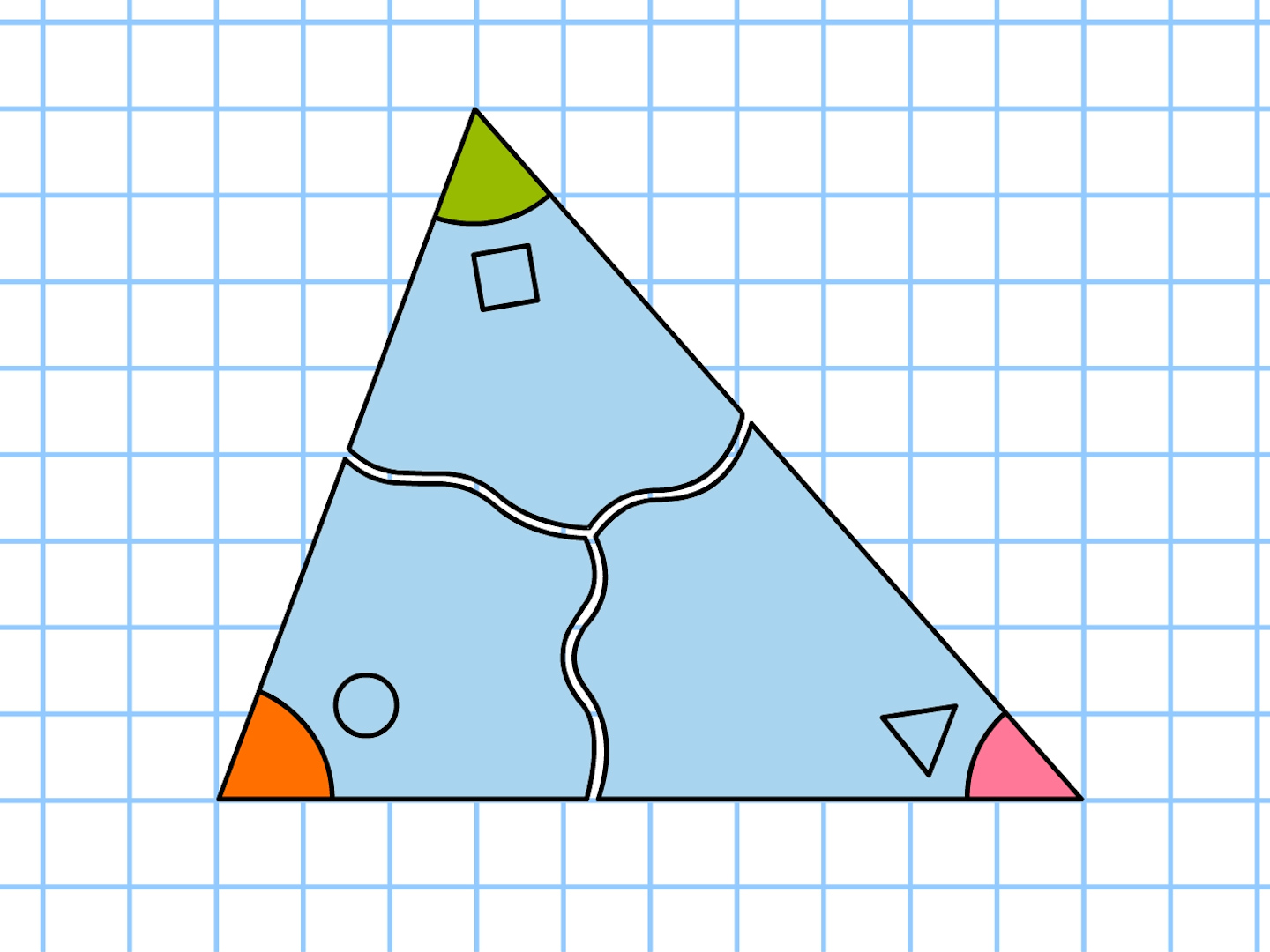



5年 三角形のふしぎ 算数イメージ動画集 大日本図書




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学




内角の和 180 N 2 外角の和 360 教遊者
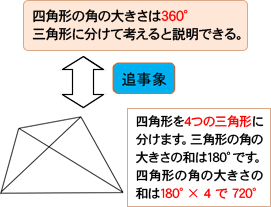



重なる形と図形の角を調べよう 図形の角と合同 第5学年 小学校 算数 My実践事例 日本文教出版




数学 中2 53 角度チャレンジ Lv 1 Youtube
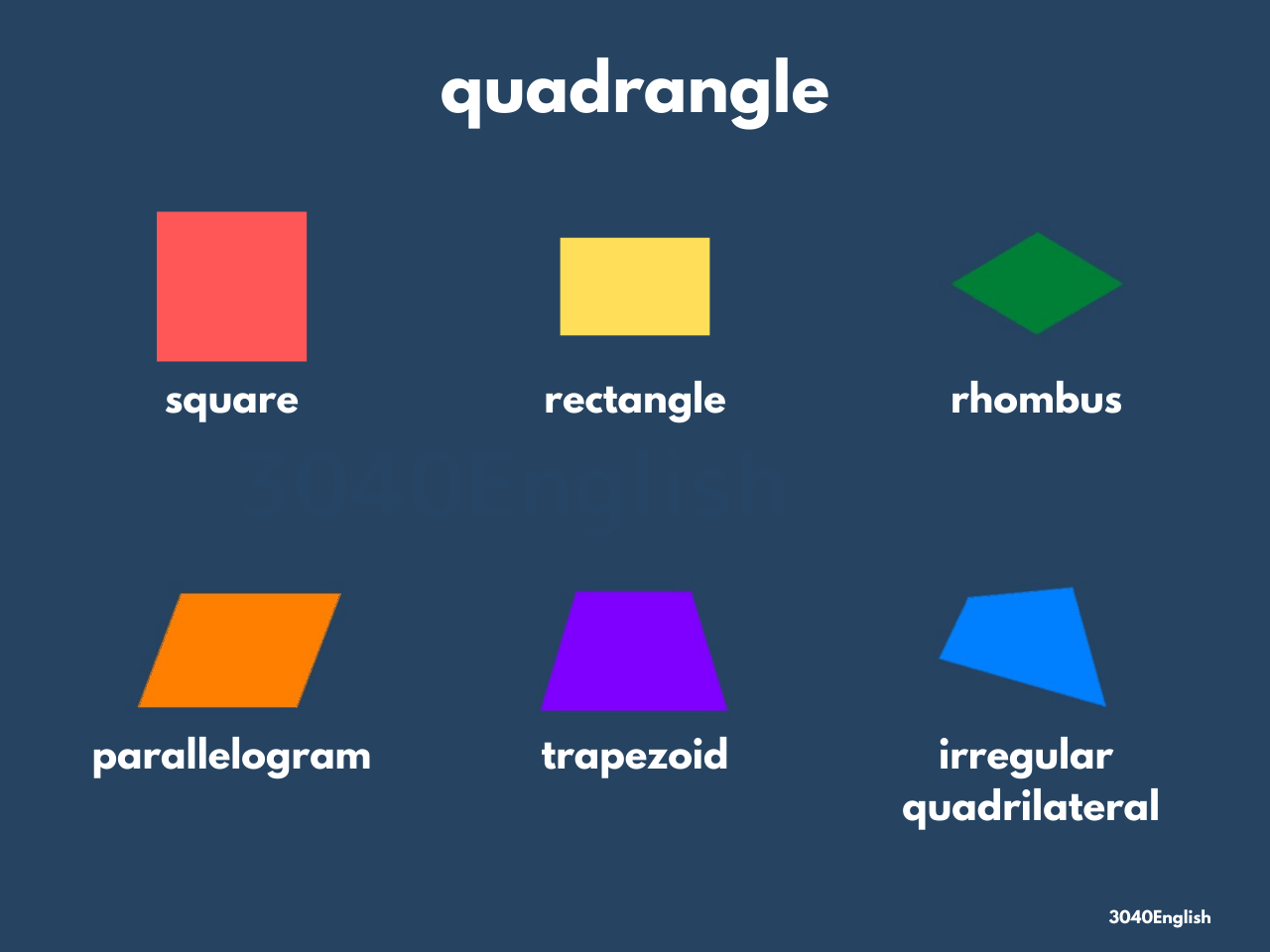



平面図形の英語表現一覧 丸 三角 長方形 正方形など 30代40代で身につける英会話




多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学



円に内接する四角形
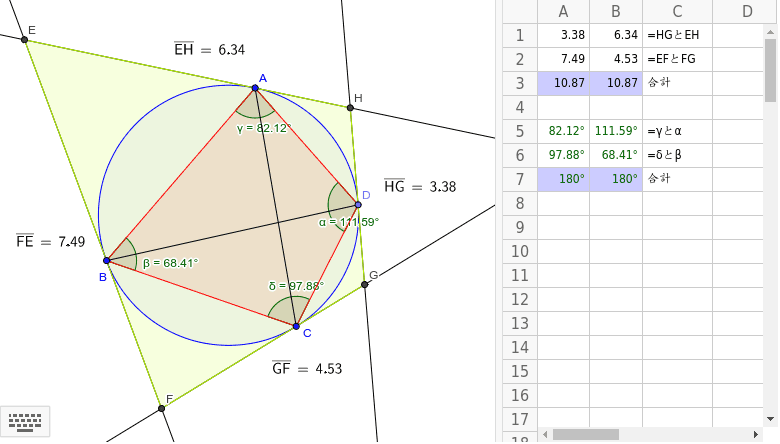



内接四角形と外接四角形 Geogebra



なぜ三角形の内角の和は180度になるのですか Quora




角度の問題です 合同な正方形を3つ横につないで長方形abcdをかきます 数学 教えて Goo
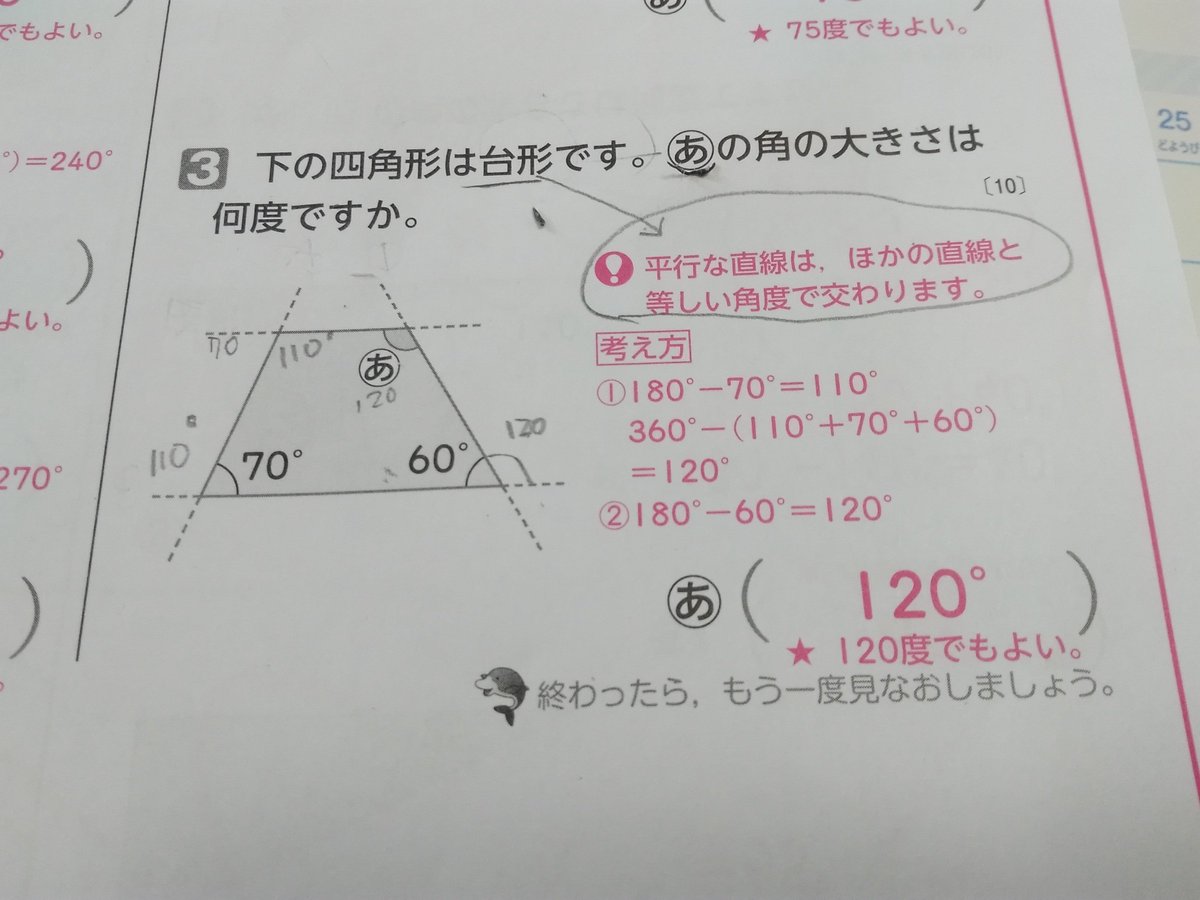



Megi メギ En Twitter 学校テストのこの問題 台形は1組の平行線が含まれるのが前提で 模範解答にも 平行な直線は他ほかの直線と等しい角度 で交わります 書いてあるのに なぜに平行線の錯覚じゃなくて 四角形の内角の和から差し引いているのかな 誰か教えて




円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ
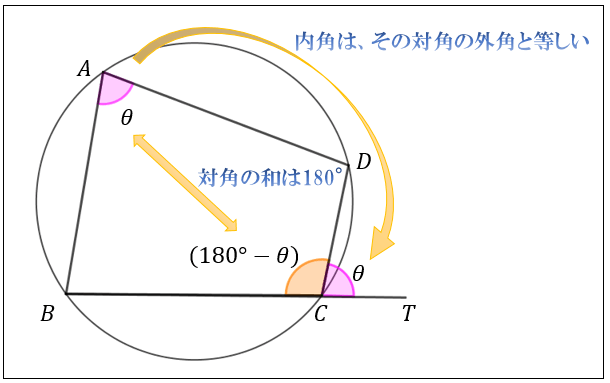



円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ




多角形の内角の和 算数の公式覚えてますか




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学



48s96ub7b0z5f Net Naisetsu Shikakukei




多角形の内角の和 は何度なのか を説明します おかわりドリル



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学




この印をつけた角の和が540になるのは何故ですか Clear



四角形の内角の和が360 であることの2通りの証明 具体例で学ぶ数学




多角形の内角の和と外角の和 三角形や四角形 五角形の角度 リョースケ大学
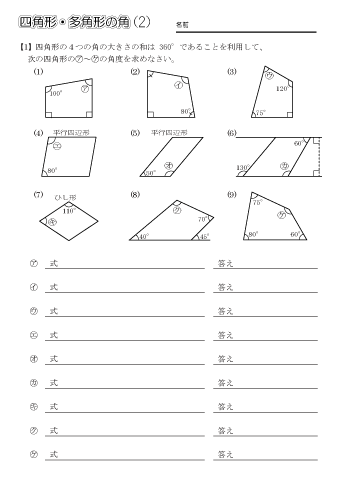



小学5年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生



1
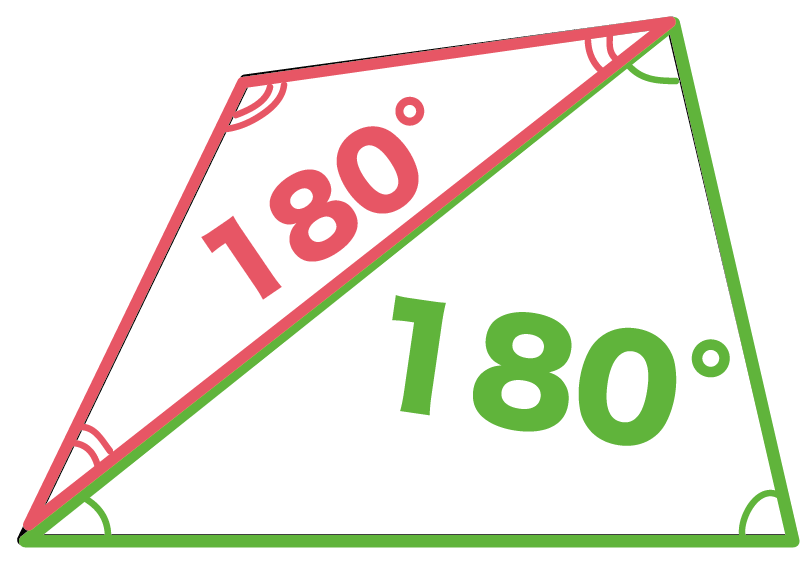



簡単公式 3秒でわかる 四角形の内角の和の求め方 Qikeru 学びを楽しくわかりやすく



小5 算数 小5 32 四角形の角 Youtube




中2数学 複雑な多角形 角の和 応用問題



Http Www Sendai C Ed Jp 02kensyu 02cyoken H27 Yoshida S Pdf
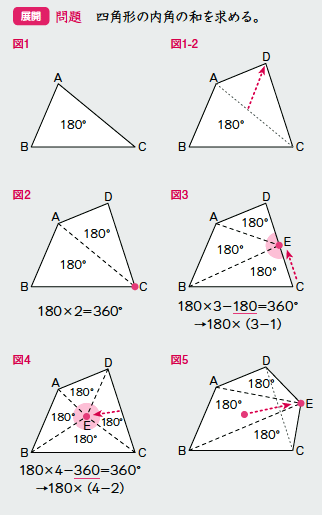



活用 の視点を取り入れた授業例 2 図形の性質 四角形の内角の和 5年生 算数における 活用 とは View21 小学版 09 Vol 2 ベネッセ教育総合研究所



内角の和 算数用語集
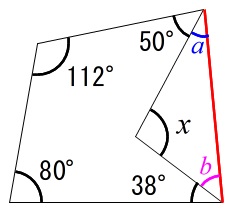



多角形の内角の和の公式と外角の和を利用した角度の求め方



0 件のコメント:
コメントを投稿